Math
algèbre
les catégories de nombres
les nombres rationnels
l’ensemble des nombres rationnels est noté \( \Bbb{Q} \). il comprend :
- les entiers naturels
\[ \Bbb{N} = \{0, 1, 2 ; …\} \]
- les entiers relatifs
\[ \Bbb{Z} = \{…; -3, -2, -1, 0, 1, 2 ; …\} \]
- les nombres décimaux.
Ce sont tous les nombres \( \Bbb{D} \) qui peuvent s’écrire sous la forme \( a \over 10^n \) avec \( a \in \Bbb{Z} \text{ et } n \in \Bbb{Z} \)
un nombre est décimal, si et seulement si, il peut s’écrire \( a \over 2^m \times 5^p \) avec \( a \in \Bbb{Z} \text{ m } \in \Bbb{N} \text{ p } \in \Bbb{N} \)
les nombres réels
un nombre réel est un nombre qui peut s’écrire avec une partie entière et un nombre fini ou infini de décimales. l’ensemble est noté \( \Bbb{R} \)
par exemple \( \pi, \sqrt{2} \)
En conséquence
\[ \Bbb{N} \subset \Bbb{Z} \subset \Bbb{D} \subset \Bbb{Q} \subset \Bbb{R} \]
les exponentielles
la fonction exponentielle est la fonction notée exp qui est égale à sa propre dérivée
$$ f’(x)=f(x) $$
$$ f(0)=1 $$
$$ e^x \cdot e^y = e^{x + y} $$
$$ \frac{e^x}{e^y} = e^{x - y} $$
$$ \frac{1}{e^x} = e^{-x}, x \in \mathbb{N} $$
$$ {e^a} = e^{b} <=> a = b $$
$$ {e^a} < {e^b} <=> a < b $$
La fonction exponentielle est dérivable sur \( \Bbb{R} \) et sa dérivée est
$$
({e^x})’ = ({e^x})
$$
identités remarquables
\[ (a+b)^2 = a^2 + 2ab + b^2\] \[ (a-b)^2 = a^2 - 2ab + b^2\] \[ (a-b)(a+b) = a^2 - b^2\]
fonctions
une fonction affine est une fonction de la forme f(x) = ay + b (c’est une droite) une fonction est paire si f(-x) = f(x) une fonction est impaire si f(-x) = -f(x)
statistique
la variance de la série statistique (S) est le nombre réel positif, noté V tel que :
\[ V = {{n_1(x_1-m)^2 + n_2(x_2-m)^2 + … + n_p(x_p-m)^2 } \over {N}} \]
L’écart-type est le nombre réel positif noté s tel que
\[ s=\sqrt(V) \]
géométrie
triangle
- la médiatrice d’un triangle est la droite qui est perpendiculaire en son milieu
- la médiane d’un triangle est la droite qui passe par le sommet et le milieu du côté opposé
- la hauteur d’un triangle est la droite qui passe par le sommet et qui est perpendiculaire au coté opposé
trigonométrie dans le triangle rectangle
Dans un triangle ABC rectangle en A
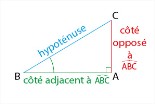
cos(A) = \( AB \over BC \) sin(A) = \( AC \over BC \) tan(A) = \( AC \over AB \)
si ABDC est un triangle rectangle en A et on note \( \alpha \) la mesure, en degré, d’un angle aigu de ce triangle, on a
\(cos^2(\alpha) + sin^2(\alpha) = 1 \)
théorème de Pythagore
un triangle ABC est rectangle en A si, et seulement si \( BC^2 = AB^2 + AC^2 \)
théorème de thalès
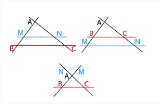
(BM) et (CN) sont 2 droites sécantes en un point A Si les droites (MN) et (BC) sont parallèles, alors \( {AM \over AB} = {AN \over AC} = {MN \over BC} \)
milieu d’un segment
pour connaitre les coordonnées du milieu d’un segment
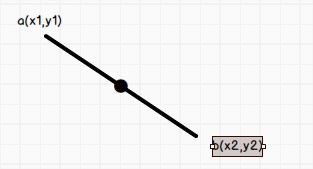
\[ \text{milieu du segment (a,b) [x, y]} = [ {{(x1+x2)} \over {2}} , {{(y1+y2)} \over {2}} ]\]
vecteur
les coordonnées du vecteur \( \vec{AB} \) sont \[ (x_{b} - x_{a} ;y_{b} - y_{a}) \]
la norme du vecteur \( \vec{u} \) notée \( \lvert| \vec{u} \rvert| \) est \[ \sqrt(x^2+y^2) \]
la distance entre les points A et B est AB = \( \lvert| \vec{AB} \rvert| \) \[ \sqrt((x_{b} - x_{a})^2 + (y_{b} - y_{a})^2) \]
les vecteurs \( \vec{u}(x;y) \) et \( \vec{v}(x’,y’) \) sont colinéaires si, et seulement si \( xy’-x’y = 0 \)
le nombre \( xy’-x’y = 0 \) est appelé déterminant du vecteur \( \vec{u} \) et du vecteur \( \vec{v} \)
3 points A, B et C sont alignés si, et seulement si, les vecteurs \( \vec{AB} \) et \( \vec{AC} \) sont colinéaires