2019-09-17

Approximation de PI par la méthode de Monte-Carlo

Par définition, $\pi$ est un nombre irrationnel $\Bbb Q$ Dans un souci de simplicité, on peut utiliser la fraction 22/7 comme approximation (très approximative !) de \(\pi\). En fouillant un peu sur Internet, on peut utilisé la fraction 355/113 un peu plus précise. Je me souviens m’être interrogé sur le sens d’une fraction pour un nombre irrationnel. La définition d’un Un nombre irrationnel est justement celle d’un nombre qui ne peut pas s’écrire sous forme de fraction. Donc pour \(\pi\), ça ne peut pas fonctionner. J’ai eu l’intuition que la résolution se faisait forcément par une suite par approximation successive et c’est là que j’ai découvert la méthode d’approximation de Monte-Carlo https://fr.wikipedia.org/wiki/M%C3%A9thode_de_Monte-Carlo

principe

La méthode de Monte-Carlo est lente, absolument pas optimisée mais très facile à comprendre pour avoir une valeur approchée de Pi.

Partons de l’hypothèse que nous avons un cercle de rayon r inscrit dans un carré de coté 2*r

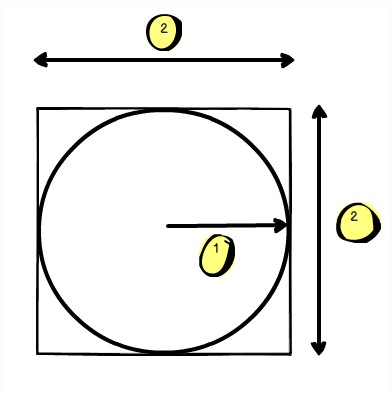
Maintenant, prenons l’hypothèse que nous projetions des points aléatoires dans notre carré. Quelle est la probabilité que le point aléatoire soit à l’intérieur du cercle ?

Cette probabilité est également à :

\[ \text{probabilité point dans le cercle} = {\text{Probabilité  dans cercle} \over \text{Probabilité dans carrée}} = {\text{Aire cercle} \over \text{aire carré}} = {{\pi r^2} \over {(2r)^2}}\]

si on cherche à simplifier \[ \text{probabilité point dans le cercle} = {{\pi r^2} \over {4r^2}}\]

on simplifie encore en supprime le \(r^2\) au numérateur et au dénominateur. Au final, la valeur de \(\pi\) est la probabilité d’être dans le cercle, multiplié par 4 !

\[ {pi} = \text{probabilité point dans le cercle} * 4 \]

implémentation

Voici un exemple de programme en Python pour déterminer cette valeur de \(\pi\)

• on crée un cercle de rayon 1 inscrit dans un carré de coté 2.
• on ajoute des points de façon aléatoire entre les valeurs -1 et 1. (le centre du cercle est le point (0,0))
• nous utilisons ensuite notre bonne vielle formule de pythagore pour savoir si notre point est à l’intérieur ou non de notre cercle.

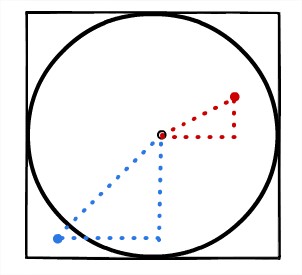
• prenons l’exemple du point rouge. Nous vérifions que la distance à l’origine x et y au carré est inférieur à 1 (rappelons que notre rayon est de 1 et que donc, le carré de l’hypothénus est égale à 1). Si oui, on peut en conclure que le point rouge est à l’intérieur du cercle.
• Dans le cas du point bleu, si on somme la distance x et y par rapport à l’origine au carré, on voit que la somme est supérieure à 1 et que donc, le point est hors du cercle
• si on prend ensuite la fraction des points à l’intérieure du cercle rapportée aux points totaux, multiplié par 4, on obtient une approximation de \(\pi\).

L’approximation met beaucoup de temps avant d’être un peu précise. Dans le programme Python ci-dessous j’affiche l’approximation tous les millions de points, donc c’est vite précis !

# approximation de PI avec la méthode de Monte-Carlo
# on prend comme hypothèse un cercle de rayon 1 inscrit dans un tableau de largeur 2

from math import pi, fabs
from random import uniform

# initialisation du nombre de points aléatoires totaux et des points inscrits dans le cercle
pointsTotaux = 0
pointsCercle = 0

# boucle infinie
while True:
    # génération d'un point aléatoire (x,y) avec des coordonnées comprises entre -1 et 1
    pointAleatoire = (uniform(-1, 1), uniform(-1, 1))

    # incrémente le nombre de points totaux
    pointsTotaux += 1

    # si le point aléatoire est situé à l'intérieur du cercle
    # la somme des carrées de ses coordonnées x et Y sont inférieures à 
    # l'hypothénus, soit le rayon du cercle
    if (pointAleatoire[0] ** 2 + pointAleatoire[1] ** 2) <= 1:
        pointsCercle += 1

    # tous les 1000000 points, on affiche les résultats
    if pointsTotaux % 1000000 == 0:
        # calcul de l'approximation de PI avec la méthode de Montecarlo
        approximationPI = pointsCercle * 4 / pointsTotaux

        # ecart par rapport à la vrai valeur de PI
        ecartPI = (1 - fabs((approximationPI - pi) / pi)) * 100
        print(
            "Nb. de points totaux : {a:2d}, Nb. de points dans le cercle {b:2d}, 
            ratio cercle*4/totaux {c:1.10f}, approximation de PI : {d:2.10f}%".format(
                a=pointsTotaux, b=pointsCercle, c=approximationPI, d=ecartPI))

exemple en p5js

j’ai écrit un exemple un peu plus visuel grâce à l’excellente librairie p5js. Cet exemple est écrit en Javascript. voici le lien https://editor.p5js.org/wilecoyote1/sketches/0WmHEd2rh

Et en direct cela nous donne :